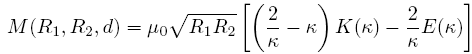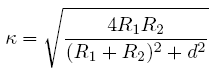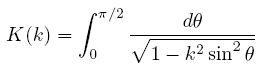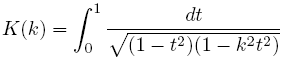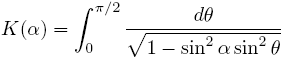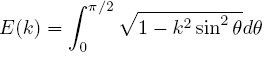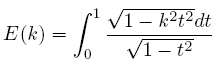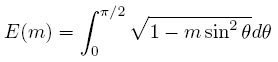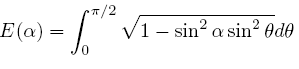Elliptical integral variable confusions

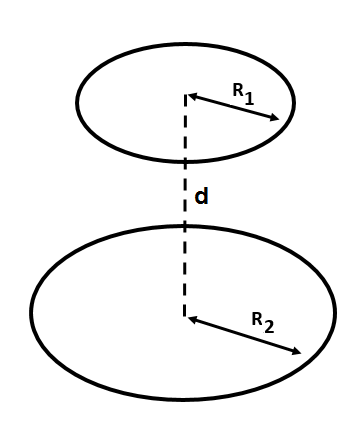
First of all, who would ever need a complete ellipitic integral? Well, I needed it for the calculation of the mutual inductance M between two circular coaxial coils.

If we consider two coils with radii R1 and R2 which are coaxilly positioned at a distance d, the mutual inductance M between them is given by:

with

K(κ) and E(κ) are the complete elliptic integrals of the first and te second kind, respectively.

Maxwell himself calculated this formula [1]. A more detailed explanation, also for non coaxial coils, can be found in [2].

I used this formula in a Matlab script, but it got me confused. Therefore, in order to clarify possible confusions with programming elliptic integrals, a short overview.

The complete elliptic integral of the first kind (represented by “K”) is defined as:

which can also be written as

The parameter k is named the elliptic modulus or eccentricity.
To complicate things, the complete elliptic integral of the first kind K is often written as:

It is the same integral, only instead of writing k², we write m, with m= k².
The parameter m is called “the parameter”.

(Seriously, they couldn’t find a better name for the parameter m then “the parameter”? They could have named it “the square of the elliptic modulus”, or “the squared eccentricity”; honestly, anything would be better than naming it “the parameter”, but I’m rambling, that’s not important).
To complicate things further, some people write the complete elliptic integral of the first kind K as:

with

The parameter α is called the modular angle.

Summarized, the complete elliptic integral of the first kind can be expressed by three parameters:
• the elliptic modulus or eccentricity k
• the parameter m
• the modular angle α

The same can be said for the complete elliptic integral of the second kind

The complete elliptic integral of the second kind (represented by “E”) is defined as:

which is sometimes expressed as:

The complete elliptic integral of the second kind E can also be written as a function of the parameter m and the modular angle α:

In Matlab, [K,E] = ellipke(m) returns the complete elliptic integral of the first and second kind. The input variable m corresponds with "the parameter" m from above! Do not use k! Also in WolframAlpha, the input variable must be m: EllipticK[m] and EllipticE[m]. The same applies for SciPy: ellipk(m) and ellipe(m), and probably a lot of other programming languages.

References:

[1] Maxwell, Electricity and Magnetism, Vol. II, §701.

[2] Zierhofer, C. M., & Hochmair, E. S. (1996). Geometric approach for coupling enhancement of magnetically coupled coils. Biomedical Engineering, IEEE Transactions on, 43(7), 708-714.